Chapter 17 Computing: Session No. 3

17.1 Objectives

The 'computing' objective is to learn how to use R to evaluate probabilities by (Monte Carlo) simulation. Taks, and the R Functions/structures used include

  • taking a sample of a specified size from the elements of a vector, either with or without replacement: sample,

  • creating a matrix from the given set of values: matrix,

  • forming a vector or array or list of values by applying a function to margins of an array or matrix: apply

  • concatenating vectors after converting to character: paste

  • creating a vector whose elements are the cumulative sums, products, minima or maxima of the elements of the argument: cumsum, cumprod , cummax and cummin

  • determining which elements of a vector or data frame are duplicates of elements with smaller subscripts, by returning a logical vector indicating which elements (rows) are duplicates: duplicated

  • removing duplicate elements/rows from a vector, data frame or array: unique,

  • stacking columns beside each other: cbind (rbind stacks rows one under the other)

The 'statistical' objective of this exercise is to learn some of the probability laws that which random processes by seeing how frequently certain events occur in computer simulations, and to deduce the laws from the (long-run) frequencies.

17.2 Exercises

17.2.1 Pooled Blood

[variation on an exercise from Chapter 3 of Colton's 1974 book Statistics in Medicine]

'Each time an individual receives pooled blood products, there is a 3% chance of his developing serum hepatitis. An individual receives pooled blood products on 45 occasions. What is his chance of developing serum hepatitis?' (JH to 1980s classes: Note that the chance is not 45 \(\times\) 0.03 = 1.35! To keep it simple, assume that there is a 3% chance that a unit is contaminated and calculate the chance that at least one of the 45 units is contaminated.)
\(\bullet\) For this computing class, simulate several sets of 45 occasions and estimate the chance that at least one of the 45 units is contaminated.
\(\bullet\) By experimentation, see if you can arrive at the formula the epi607 students in the 1980s would have used.
\(\bullet\) By repeating the process with the same number of simulations (the same N.SIMS value), and then experimenting with this same number, come up with a rule of thumb for the number of simulations (the N.SIMS value) needed for you to 'trust' the first decimal place in your (Monte Carlo) estimate of the true probability.

n.times = 45 ; prob.per.time = 0.03 ; N.SIMS = 100
sims = matrix(sample(c("+","-"),
                     size=N.SIMS*n.times,
                     prob=c(prob.per.time,1-prob.per.time),
                     replace=TRUE),
              N.SIMS, n.times) # N.SIMS rows, n.times columns
noquote(apply(sims[1:10,],1,paste,collapse=""))
##  [1] ---------------------------------------------
##  [2] -------+-------------------------+-+---------
##  [3] ---------------------------+---------------+-
##  [4] +---------------------------------------+----
##  [5] -------------------------+-------------------
##  [6] ---------------------------------------------
##  [7] -+--+----------------------------------------
##  [8] ----+----------------------------------------
##  [9] ---------------------+-----------------------
## [10] ------------------+--------------------------
str(sims)
##  chr [1:100, 1:45] "-" "-" "-" "+" "-" "-" "-" "-" "-" "-" "-" "-" "-" "-" ...
positive = apply(sims=="+",1,any)  # applies the 'any' function to each row
str(positive)
##  logi [1:100] FALSE TRUE TRUE TRUE TRUE FALSE ...
proportion.of.sims.with.a.hit = mean(positive)
num = sum(positive) 

cat(paste("Proportion.of.sims.with.a.hit: ",toString(num),"/",toString(N.SIMS)," = ",toString(proportion.of.sims.with.a.hit),";\nfor a more stable estimate, use a larger N.SIMS",sep=""))
## Proportion.of.sims.with.a.hit: 69/100 = 0.69;
## for a more stable estimate, use a larger N.SIMS

17.2.2 Life Tables [1990]

The following [conditional] probabilities are taken from the abridged life tables for males (M) and females (F) computed from mortality data for Québec for the year 1990, and published by the Bureau de la statistique du Québec: [the probabilities for 90-year olds have been modified!].
In a (current) life table, one takes current (in this case 1990) i.e. cross-sectional death rates and applies them to a fictitious cohort to calculate what % of the cohort would survive past various birthdays -- if die these rates persisted -- and to calculate the average age at death (also known as life expectancy at birth).

........ Probability that a person who lives to his/her
........ x-th birthday will die during next 10 years

.......x .... .M ....... F
...... 0 ... 0.010 ... 0.008
..... 10 ... 0.006 ... 0.002
..... 20 ... 0.012 ... 0.004
..... 30 ... 0.016 ... 0.007
..... 40 ... 0.031 ... 0.017
..... 50 ... 0.080 ... 0.042
..... 60 ... 0.211 ... 0.104
..... 70 ... 0.448 ... 0.259
..... 80 ... 0.750 ... 0.585
..... 90 ... 1.000 ... 1.000

  • Fill in the blanks in the following diagram, which shows the proportions of males and females who survive past their xth birthday (x = 0, 10, 20, 30, ... 100) (these plots are called survival curves).

  • Calculate, by successive subtractions^ or otherwise, the [unconditional] proportions [i.e. proportions of the entire cohort] who will die between their xth and x+10th birthdays (x = 0, 10, 20, 30, ... 90). Plot them as histograms. In a later exercise, we will use these proportions to calculate life expectancy.

e.g.
Pr[Die after 70th birthday] = 0.wwww
Pr{Die after 80th birthday] = 0.zzzz
Pr[die between 70 and 80] = difference

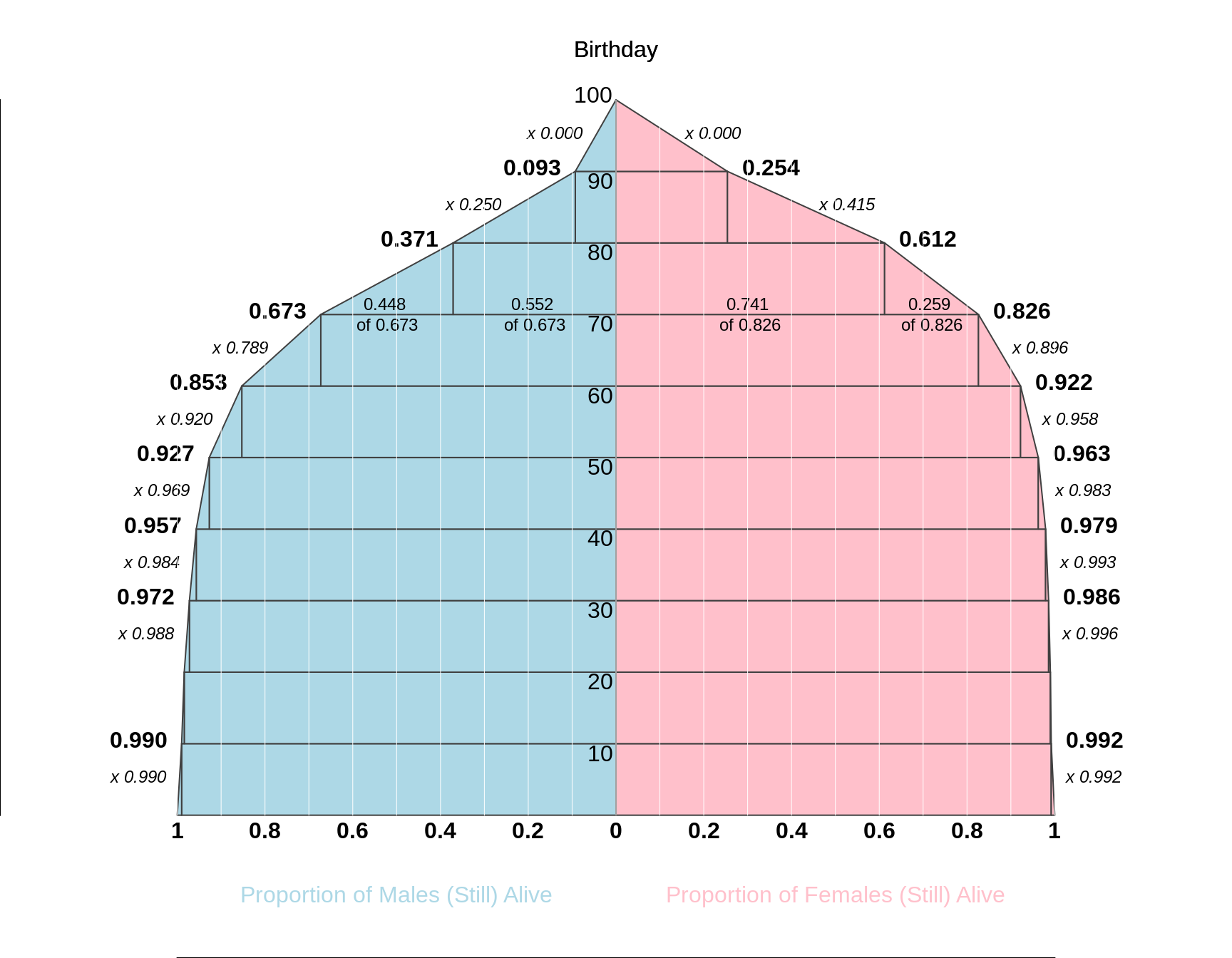
Life Tables based on abbreviated data from 1990 given in above table. The tabular orientation is 'bottom-up' rather than the conventional 'top-down' format, and side by side, in the spirit of population 'pyramids'. Also unusually, the 'survival surve' for males has the surviving proportion on the horizonatl axis, and the ages on the vertiacl axis. But if you were to rotate it by 90 degrees to the right, it would have conventional survival curve orentation.

Figure 17.1: Life Tables based on abbreviated data from 1990 given in above table. The tabular orientation is 'bottom-up' rather than the conventional 'top-down' format, and side by side, in the spirit of population 'pyramids'. Also unusually, the 'survival surve' for males has the surviving proportion on the horizonatl axis, and the ages on the vertiacl axis. But if you were to rotate it by 90 degrees to the right, it would have conventional survival curve orentation.

For population pyramids, see https://www.populationpyramid.net/world/2019/

For dynamic ones, see https://www12.statcan.gc.ca/census-recensement/2016/dp-pd/pyramid/pyramid.cfm?geo1=01&type=1

17.2.3 Life Tables [2018]

For males and females separately, extract the 22 [conditional] probabilities of dying within the (1, 4 or 5 year) age intervals shown in Table 3.9 of this Institut de la statistique du Quebec report. They can be found in the \(q_x\) column [ x: age; q\(_x\) : given survival to birthday x, probability of dying between birthday x and birthday x+a, where a, a=1, 4 et 5.]

  • Use these to compute the surviving fractions at each of the birthdays shown in Table 3.9. As a double check on your answers, you have the \(l_x\) columns in Table 3.9 [l\(_x\): number surviving at x-th birthday.] Hint: instead of using a loop, you can use the 'cumulative product' function cumprod. For example, cumprod(c(0.9, 0.8, 0.7)) yields the vector of length 3, namely 0.9, 0.9 \(\times\) 0.8 = 0.72, and 0.9 \(\times\) 0.8 \(\times\) 0.7 = 0.504.
  • Plot the fractions against the ages, overlaying one curve on the other. Make sure to label the axes appropriately, and using large enough lettering that people at the right hand of the age scale, where most of the action is, can read them.
  • Visually measure the median survival for each gender.
  • Do you think the mean survival (the life-expectancy at birth) is smaller or larger than the median? Explain your reasoning.
  • The best way to be sure is to have and plot the frequency distributions of the ages at death. Using the same logic as in question 2, derive these frequencies, and plot them. Note that the first 2 age-bins are narrower than the others, so make wahtever adjustments are needed.
  • Why don't these frequency distributions match those shown in Figure 3.5 of the report?
  • Examine Figure 3.15 of the report, and explain why life expectancies calculated from single-calendar-year data can 'wobble' quite a bit from year to year.

17.2.4 A simplified epidemic

[from Mosteller and Rourke Book]

An infectious disease has a one-day infectious period, and after that day the person who contracts it is immune. Six hermits (numbered 1,2, 3, 4, 5, 6, or named A-F) live on an island, and if one has the disease he randomly visits another hermit for help during his infectious period. If the visited hermit has not had the disease, he catches it and is infectious the next day. Assume hermit 1 has the disease today, and the rest have not had it. In the pre-R era students were asked to throw a die to choose which hermit he visits (ignore face 1) Today you are asked to use the sample function in R to choose which hermit he visits. That hermit is infectious tomorrow. Then 'throw' (or use R) again to see which hermit he visits, and so on. Continue the process until a sick hermit visits an immune one and the disease dies out.

  • Repeat the 'experiment' several times and find
  • the average number who get the disease

  • the probability that (the proportion of experiments in which) everyone gets the disease.

  • Try to figure out a closed-form (algebraic) expression for the answer to the second part.

one.random.sequence =function(n.hermits=6){ # max 26, for 1-letter names
    names = LETTERS[1:n.hermits]
    who.is.infectious.today = 1
    trail = names[who.is.infectious.today]
    for(visit in (1:(n.hermits-1)) ) {
        who.infectious.hermit.visits = 
         sample( (1:n.hermits)[-who.is.infectious.today], 1)
       trail = c(trail, names[who.infectious.hermit.visits])
    }
    return(trail)
}

(s = one.random.sequence(6)) ; duplicated(s)
## [1] "A" "F" "E" "E" "E" "B"
## [1] FALSE FALSE FALSE  TRUE  TRUE FALSE
N.SIMS = 100; n.hermits = 6
sequences  = matrix(NA,N.SIMS,n.hermits)
for(i.row in 1:N.SIMS ){
   sequences[i.row,1:6] = one.random.sequence(n.hermits)
}

first.duplicate = function(x){
   d = duplicated(x)
   result = length(x)+1 
   if(any(d)) result = min( (1:n.hermits)[duplicated(x)] )
   return(result)
} 

when.first.dup.happens = apply(sequences,1,first.duplicate)

table(when.first.dup.happens)
## when.first.dup.happens
##  3  4  5  6  7 
## 21 39 23 16  1

17.2.5 Screening for HIV

See Figure 1 'Meaning of Positive HIV Tests for HIV') in the article Can we afford the false positive rate?

  • Use R to redraw their Figure

  • Add on top of it a curve for a population with a 1% prevalence.

  • Add a curve for a prevalence of 0.16%, but assuming sensitivity is only 90%.

17.2.6 Duplicate Birthdays

[The exercises are found at the end of this sub-section]

For 13 years in the 607 course from 1981 to 1993, JH handed out a page with a 12 x 31 grid and asked the students to indicate their birthday (month and day). The numbers of students in the class ('n') varied from 19 to 52 (mean 32, median 33) The results, in 'raw' form here, may surprize you. In 10 of the 13 classes, there was at least one duplicate birthday.

http://www.medicine.mcgill.ca/epidemiology/hanley/Reprints/LotteriesProbabilitiesHANLEY1984TeachingStatistics.pdf#page=3

By the way, the 'Birthday Problem' is a classic in probability classes.

year=c(0.8+(1981:1984),0.8+(1986:1988),
       1989.4,1989.8,0.4+(1990:1992),1993.8)
n = c(27,37,33,20,21,19,39,31,31,52,43,49,32)
at.least.one.duplicate.birthday =
   c(TRUE,TRUE,TRUE,FALSE,TRUE,FALSE,TRUE,TRUE,
     FALSE,TRUE,TRUE,TRUE,TRUE) 
cbind(year,n,at.least.one.duplicate.birthday)
##         year  n at.least.one.duplicate.birthday
##  [1,] 1981.8 27                               1
##  [2,] 1982.8 37                               1
##  [3,] 1983.8 33                               1
##  [4,] 1984.8 20                               0
##  [5,] 1986.8 21                               1
##  [6,] 1987.8 19                               0
##  [7,] 1988.8 39                               1
##  [8,] 1989.4 31                               1
##  [9,] 1989.8 31                               0
## [10,] 1990.4 52                               1
## [11,] 1991.4 43                               1
## [12,] 1992.4 49                               1
## [13,] 1993.8 32                               1
sum(at.least.one.duplicate.birthday)
## [1] 10
cat("n's in the classes without a duplicate:")
## n's in the classes without a duplicate:
n[!at.least.one.duplicate.birthday]
## [1] 20 19 31

Leaving out people born on Feb. 29, and assuming [FOR NOW] all of the 365 birthdays are equally likely, we have the following formula for the probability of NO duplicate birthday in a sample of \(n\). By subtracting this probability from 1 (a common 'trick' when working with the probability of 'at least' ... ), we obtain the probability of AT LEAST ONE duplicate birthday:

\[Prob[all \ n \ birthdays \ are \ different] = \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \dots \times \frac{365-(n-1)}{365}.\]

Let's work this out (or tell R to work it out) for n's all the way from 1 to 365, and show the probabilities for the 13 classes, overlaid on all of the probabilities for \(n\) from 1 to 60.

prob.all.n.different = cumprod( (365:1) / rep(365,365) )

prob.all.different = round(prob.all.n.different[n],2)
prob.at.least.1.duplicate = 1 - prob.all.different

par(mfrow=c(1,1),mar = c(4.5,5,0,0))
plot(1:60,prob.all.n.different[1:60],type="l",
     cex.axis=1.25,cex.lab=1.25,
     xlab="n",col="blue",ylab="Probability")

abline(h=seq(0,1,0.1),col="lightblue")
abline(h=0.5,col="lightblue",lwd=2)
abline(v=seq(0,60,5),col="lightblue")

lines(1:60,1-prob.all.n.different[1:60],col="red")

points(n,prob.all.different,pch=19,cex=0.5)
points(n,1-prob.all.different,pch=19,cex=0.5)

points(n,at.least.one.duplicate.birthday,
       pch="X",cex=1.0,
       col=c("blue","red")[1+at.least.one.duplicate.birthday])

text(35,1-prob.all.n.different[35],
     "Prob. at least 1 duplicate",
     cex=1.5,col="red",adj=c(0,1.25))

text(35,prob.all.n.different[35],
     "Prob. all n are different",
     cex=1.5,col="blue",adj=c(0,-0.25))

Why is the probability so much higher than you would naively think?

If in a class of 30, we ask you what the probability is, you are likley to reason like this ...

'30 out of 365, so about 1 chance in 12 or so, or about 8%'.

BUT, by reasoning this way, you are just thinking about the probability that YOUR birthday will match the birthday of someone else. But then EVERYONE ELSE has to go through the same calculation, so there are a lot of possibilities for a match, between someone else and someone else.

An easy way to appreciate the large number opportunities there are for a match is to look at a random sample of 30 birthdays, and see if they contain a match. If you can't sort them first, you will have to compare the 2nd with the 1st (thats 1), the 3rd with the 1st and the 2nd (2 more), the 4rd with the 1st and the 2nd and 3rd (3 more), and so on, so 1 + 2+ ... + 29 = 435 in all! But if you are the first to call out your birth, and then look/listen for a match with YOUR birthday, thats just 29 others. So instead of 1/12, the probability of SOME match (anyone with anyone else) os a LOT higher than 1/12. (From the blue graph, it's about 70%!).

all.birthdays =
read.table(
   "http://www.biostat.mcgill.ca/hanley/statbook/BirthdayProbabilities.txt",
   as.is=TRUE)

# (as.is=TRUE doesn't convert alphabetic variables into factors)

plot(1:366,all.birthdays$prob,
      ylim=c(0,max(all.birthdays$prob)),
      cex = 0.5,pch=19,
      xlab="Days of Year (1=Jan 1, 366=Dec 31)")
abline(h= c(0, 1/(365:366)))
abline(v= seq(0,366,30),col="lightblue")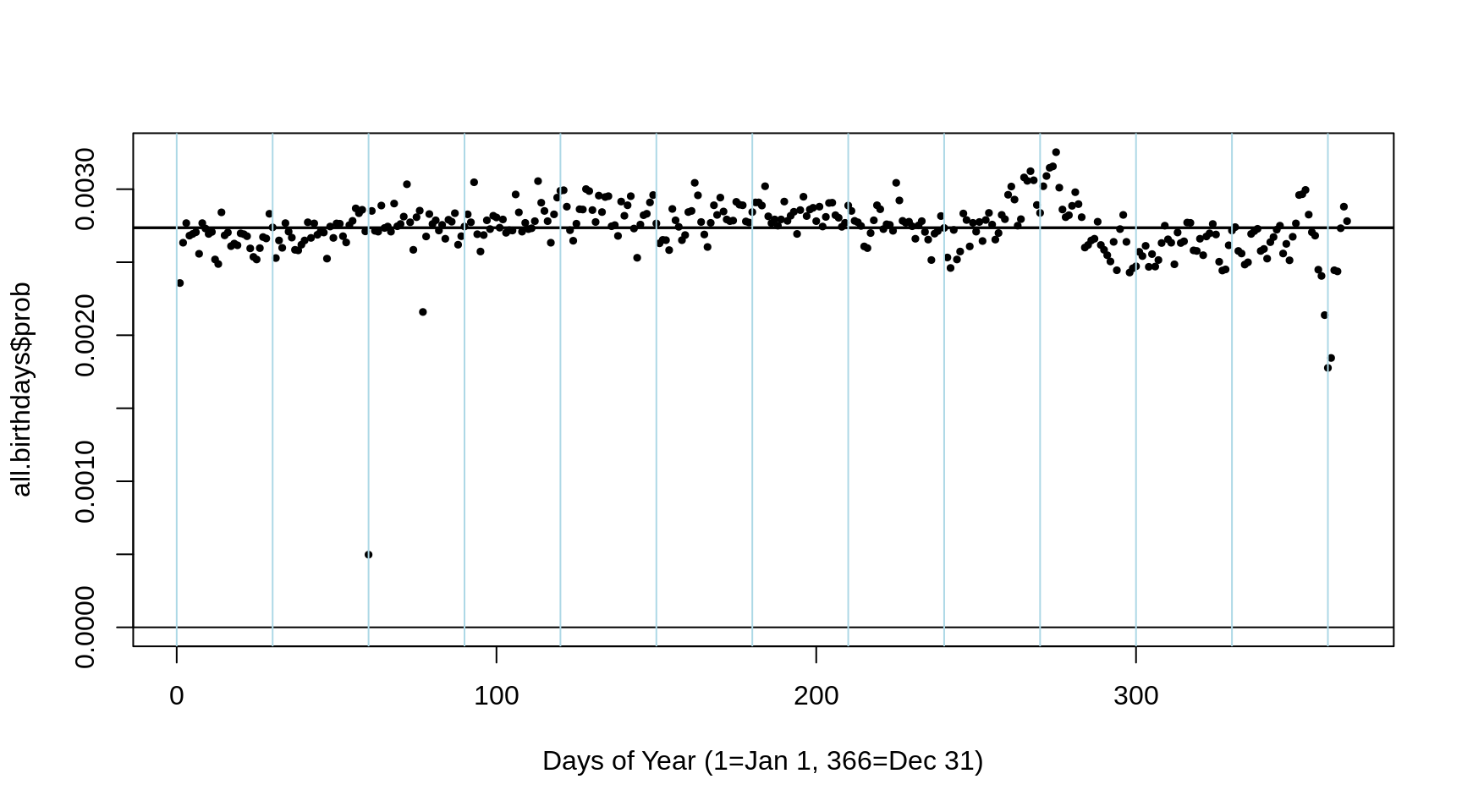

sample.of.30 = sample(all.birthdays$Birthday,30,replace=TRUE)

noquote(sample.of.30)
##  [1] Jun 20 Mar 16 Mar 09 Oct 16 Jun 04 Mar 13 Oct 14 Nov 11 Feb 26 May 16
## [11] Feb 14 Jul 03 Jun 26 Apr 24 Jun 23 Sep 06 May 21 Nov 10 Jul 20 Apr 23
## [21] Oct 01 Mar 04 Jan 29 Dec 27 Aug 24 Jan 12 Aug 28 Aug 22 Oct 05 May 23

If you have the software, you would sort this list first,

noquote( sort(sample.of.30) )
##  [1] Apr 23 Apr 24 Aug 22 Aug 24 Aug 28 Dec 27 Feb 14 Feb 26 Jan 12 Jan 29
## [11] Jul 03 Jul 20 Jun 04 Jun 20 Jun 23 Jun 26 Mar 04 Mar 09 Mar 13 Mar 16
## [21] May 16 May 21 May 23 Nov 10 Nov 11 Oct 01 Oct 05 Oct 14 Oct 16 Sep 06

so its easier to spot any duplicates. And, if this is too laborious to do manually, you can use the unique and duplicated functions in R

unique.birthdays = unique(sample.of.30) 
( n.unique = length(unique.birthdays) )
## [1] 30
duplicated(sample.of.30)
##  [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [13] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [25] FALSE FALSE FALSE FALSE FALSE FALSE
( sample.of.30[ duplicated(sample.of.30) ] )
## character(0)

But, as computer science people will tell you, sorting large lists takes a lot of computing. Just think about how you would manually sort a list of 1 million or 1 billion! The book Algorithms to Live By explains this well.

In the early 1980s, Loto Quebec did not realize that there is a high chance of duplicates when the sample size is sizeable, and, as we tell in our case III, they were embarrassed. We tell more of the story here. They now SORT the list first, to find duplicates.

Exercises

  • By splitting 4 successive nodes into FirstDuplicate = YES or NO, draw a probability tree for the first 4 birthdays announced (Such a tree, with each node splitting into an Infected hermit visit a Susceptible hermit or visit an immune/recovered hermit, can help you think through the simulated mini-epidemic. BTW: you hear a lot abot SIR models thse days, and you will have seen the 'R' category displated in many of the covid-19 epidemic graphs)
  • Using the prob.all.n.different vector derived above, calculate, by successive subtractions^ or otherwise, the probability that the first duplicate will show up on the [\(Y\) =] 2nd, 3rd, ... birthday announced. Plot the frequency distribution of \(Y\).
  • By simulation, estimate the probability that 'in 20 draws one will not obtain a duplicate' ^^.
  • In every class where this Birthday Problem is addressed, students object that leaving out Feb 29 and assuming all of the 365 birthdays are equally likely are not realistic. Births vary somewhat by season and more so by day of the week So, in reality, are the probabilities of at least one duplicate birthday higher or lower than you have calculated above? Or is it impossible to say in which direction they are moved?
    To investigate this use the all.birthdays dataset created in the R code above. you can visualize the variation in the 366 probabilites by using this statement plot(1:366,all.birthdays$prob, ylim=c(0,max(all.birthdays$prob)), cex = 0.5,pch=19, xlab="Days of Year (1=Jan 1, 366=Dec 31)") and drawing grids with these ones abline(h= c(0, 1/(365:366))) and abline(v= seq(0,366,30),col="lightblue").
    This distribution is based on all births in a certain country from 1990-1999 [the years when many of you were born]. From it, draw several samples of 20 birthdays, and calculate the proportion of these sets in which the 20 birthdays are unique, and conversely, contain at least 1 duplicate. Some R code is given below.
  • Try to figure out from the features of the plot what country the birthday data are from? Explain your reasoning.
  • Just from how much the 366 probabilities 'wobble' around 1/365 or 1/366, try to figure out (approximately, to within an order of magnitude) how many births were used to derive the 366 proportions. For example, is it a country with a population size such as China, India, USA, Germany, New Zealand, Iceland, Prince Edward Island, the Yukon Territory, etc?

https://rss.onlinelibrary.wiley.com/doi/full/10.1111/j.1740-9713.2013.00705.x

^ If \(Y\) = which draw produces 1st duplicate (so \(Y\) = 2,... 365). e.g.

Pr[$Y$ > 6] = Pr[Y = 7 or 8 or 9 or .. or 365 ]
Pr[$Y$ > 7] = Pr[Y = .... 8 or 9 or .. or 365 ]
Difference: = Pr[Y = 7]

N.SIMS=100
n = 23
#PROBS = rep(1/366,366)    # ON  for comparison
PROBS  = all.birthdays$prob # OFF for comparison
B = matrix(     
      sample(all.birthdays$Birthday,
             size = N.SIMS*n,
             prob = PROBS,
             replace=TRUE),
      nrow = N.SIMS,  ncol = n)
head(B,2)
##      [,1]     [,2]     [,3]     [,4]     [,5]     [,6]     [,7]     [,8]    
## [1,] "Feb 09" "Jul 09" "Apr 02" "Sep 17" "Nov 27" "Oct 28" "Oct 16" "May 25"
## [2,] "Jul 17" "Mar 21" "Nov 29" "Jun 20" "Apr 03" "Dec 13" "Jan 18" "Jun 04"
##      [,9]     [,10]    [,11]    [,12]    [,13]    [,14]    [,15]    [,16]   
## [1,] "Feb 28" "Apr 24" "Nov 21" "Jun 05" "Jun 20" "Feb 08" "Jun 03" "Nov 30"
## [2,] "Jan 13" "Aug 21" "Feb 08" "Dec 06" "Aug 12" "Dec 06" "Nov 11" "May 10"
##      [,17]    [,18]    [,19]    [,20]    [,21]    [,22]    [,23]   
## [1,] "Jul 31" "Sep 18" "Oct 20" "May 16" "May 22" "Jan 02" "Nov 26"
## [2,] "Aug 07" "Nov 11" "Dec 14" "Dec 23" "Jul 28" "Oct 24" "Feb 13"
duplicate = apply(B,1,
   function(x) sum(duplicated(x)) > 0 )

noquote(paste(sum(duplicate), "duplicates /", 
   N.SIMS,
   " ; larger N.SIMS: more precise probability estimate.",collapse=" "))
## [1] 52 duplicates / 100  ; larger N.SIMS: more precise probability estimate.

17.2.7 Chevalier de Méré

[see here}(https://www.cut-the-knot.org/Probability/ChevalierDeMere.shtml) or
Gamblers in 17th century France used to bet on the event of getting at least one 1 'six' in four rolls of a die or in 1 roll of 4 dice [dice is plural for die]. As a more trying variation, two dice were rolled 24 times with a bet on having at least one double six. Chevalier de Méré who expected a couple of sixes to turn up in 24 double rolls with the frequency of a six in 4 single rolls. However, he lost consistently.

  • Simulate a large number of each of these games, and estimate the probability of getting (a) at least one six in four rolls of a dice (b) at least one "double six" when a pair of dice is thrown 24 times

  • Why does it take a large number of simulations to determine which game offers the better chance of winning?

  • Can you work out the probabilities directly?

  • https://www.casino-games-online.biz/dice/chevalier-de-mere.html

17.3 Other Exercises (under construction)

17.3.1 HIV transmission

[ probability per act ]

Napoleon

Minard http://euclid.psych.yorku.ca/www/psy6135/tutorials/Minard.html

Efron Monty Hall

  1. The Economist

  2. Wald : CF screening

  3. OJ p-value

  4. Adult soccer ball.. wrong probability

  5. Vietnam deaths

  6. NHL birthdays

Buffon's needle

Estimating Pi

Similar

Adult size soccer ball

Medical School admission rates, by gender.

Vietnam war deaths, by month of birth

NHL success, by month of birth

John Snow, cholera deaths South London, by source of drinking water

Galton

Greenwood

Mosteller

Ages of books

ngrams

  1. Prob of
  • duplicate birthdays in a sample of \(n\) persons
  • surviving from 80th to 85th birthday if the (conditional) 1-year at a time proportions dying (risks) are ...
  • Chevalier de Méré no 6, at least 1 six.
  1. Variation with and without constraints

-3- "Duplicate Numbers" [mini-version of birthday problem] To appreciate the high probability of duplicate birthdays, take a simpler case of drawing single digit numbers at random from a Random Number Table or spreadsheet until one gets a duplicate. (also, try actually doing it to see how many draws it takes) a Calculate the probability that in 5 draws one will not obtain a duplicate, i.e., the probability of a sequence 1st# ; 2nd# [≠ 1st#] 3rd# [≠ 2nd# ≠ 1st#] 4th# [≠ 3rd# ≠ 2nd# ≠ 1st#] 5th# [≠ 4th# ≠3rd# ≠ 2nd# ≠ 1st#] b Calculate, by successive subtractions* or otherwise, the probability that the first duplicate will show up on the [Y =] 2nd, 3rd, ...11th draw. Plot the frequency distribution of the # draws, Y, until a duplicate.

Ice Breakup Dates

Here are some details on the Nenana Ice Classic More here

17.3.2 The 2018 Book of Guesses

We are keen to establish the distribution of guesses, with the guessed times measured from midnight on December 31, 2017. Thus a guess of April 06, at 5:15 p.m. would be measured as 31 + 28 + 31 + 5 + 12/24 + (5+ 15/60)/24 = 95.71875 days into the year 2018.

It would be tedious to apply optical character recognition (OCR) to each of the 1210 pages in order to be able to computerize all 240,000 guesses. Instead, you are asked to reconstruct the distribution of the guesses in two more economical ways:

  • By determining, for (the beginning of) each day, from April 01 to June 01 inclusive, the proportion, p, of guesses that predede that date. [ In R, if p = 39.6% of the guesses were below 110 days, we would write this as pGuessDistribution(110) = 0.396. Thus, if we were dealing with the location of a value in a Gaussian ('normal') distribution, we would write pnorm(q=110, mean = , sd = ) ] Once you have determined them, plot these 62 p's (on the vertical axis) against the numbers of elapsed days (90-152) on the horizontal axis.

  • By determining the 1st, 2nd, ... , 98th, 99th percentiles. These are specific examples of 'quantiles', or q's. The q-th quantile is the value (here the elapsed number of days since the beginning of 2018) such that a proportion q of all values are below this value, and 1-q are above it. [ In R, if 40% of the guesses were below 110.2 days, we would write this as qGuessDistribution(p=0.4) = 110.2 days. Thus, if we were dealing with the 40th percentile of a Gaussian distribution with mean 130 and standard deviation 15, we would write qnorm(p=0.4, mean = 130, sd = 15). ] Once you have determined them, plot the 99 p's (on the vertical axis) against the 99 (elapsed) times on the horizontal axis.

  • Compare the Q\(_{25}\), Q\(_{50}\), and Q\(_{75}\) obtained directly with the ones obtained by interpolation of the curve showing the results of the other method.

  • Compare the directly-obtained proportions of guesses that are before April 15, April 30, and May 15 with the ones obtained by interpolation of the curve showing the results of the other method.

  • By successive subtractions, calculate the numbers of guesses in each 1-day bin, and make a histogram of them. From them, calculate the mean, the mode, and the standard deviation.

To measure the spread of guesses, Galton, in his vox populi (wisdom of crowds) article, began with the interquartile range (IQR), i.e. the distance between Q75 and Q25, the 3rd and 1st quartiles. In any distribution, 1/2 the values are within what was called the 'probable error (PE) of the mean; i.e., it is equally probable that a randomly selected value would be inside or outside this middle-50 interval. Today, we use standard deviation (SD) instead of probable error. In a Gaussian distribution, some 68% of values are within 1 SD of the mean, whereas 50% of values are within 1 PE of the mean. We can use R to figure out how big a PE is in a Gaussian distribution compared with a SD. By setting the SD to 1, and the eman to 0, we have

Q75 = qnorm(p = 0.75, mean=0, sd=1)
round(Q75,2)
## [1] 0.67

i.e, a PE is roughtly 2/3rds of a SD.

  • Galton -- convert to SD.

  • Geometric mean Amsterdam study

  • How far off was the median guess in 2018 from the actual time? Answer in days, and (with reservations stated) as a percentage?

  • Why did the experts at the country fair do so much better?

  • Where were the punters in 2019 wrt the actual ?

https://www.technologyreview.com/s/528941/forget-the-wisdom-of-crowds-neurobiologists-reveal-the-wisdom-of-the-confident/

https://www.all-about-psychology.com/the-wisdom-of-crowds.html

http://galton.org/essays/1900-1911/galton-1907-vox-populi.pdf

[Nenana Ice Classic]

Tanana River